BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: An Example from Mechanics: Damping
Up: The Exponential Function
Previous: The Exponential Function
Figure:
The functions ex, e-x, 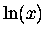 and 1/x
plotted on the same graph over the range from x=0 to x=4.
Note that
and 1/x
plotted on the same graph over the range from x=0 to x=4.
Note that 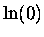 is undefined.
[There is no finite power to which we can raise e and get zero.]
Similarly, 1/x is undefined at x=0, while
1/(-x) = - 1/x.
Also,
is undefined.
[There is no finite power to which we can raise e and get zero.]
Similarly, 1/x is undefined at x=0, while
1/(-x) = - 1/x.
Also,
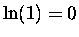 [because any number raised to the zeroth power equals 1 -
you can easily check this against the definitions]
and
[because any number raised to the zeroth power equals 1 -
you can easily check this against the definitions]
and 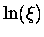 [where
[where 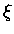 any positive number less than 1] is negative.
However, there is no such thing as the natural logarithm
of any negative number.
any positive number less than 1] is negative.
However, there is no such thing as the natural logarithm
of any negative number.
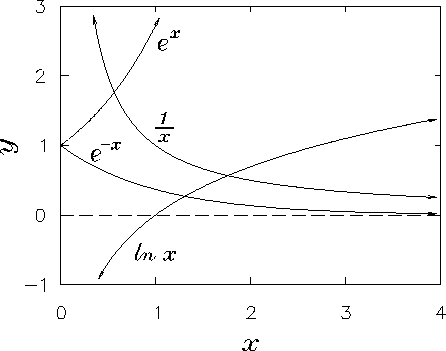 |
Our formula (21) for the real value of your dollar as
a function of time is the only function which will
satisfy the differential equation (2) from which we started.
The exponential function is one of the most useful of all
for solving a wide variety of differential equations.
For now, just remember this:
Whenever you have
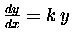 ,
you can be sure that
,
you can be sure that
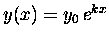 where y0 is the ``initial value'' of y [when x=0].
Note that k can be either positive or negative.
where y0 is the ``initial value'' of y [when x=0].
Note that k can be either positive or negative.
Finally, note
the property of the second derivative:
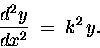 |
(26) |
We will see another equation almost like this
when we talk about SIMPLE HARMONIC MOTION.


Next: An Example from Mechanics: Damping
Up: The Exponential Function
Previous: The Exponential Function
Jess H. Brewer
1998-08-04
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE 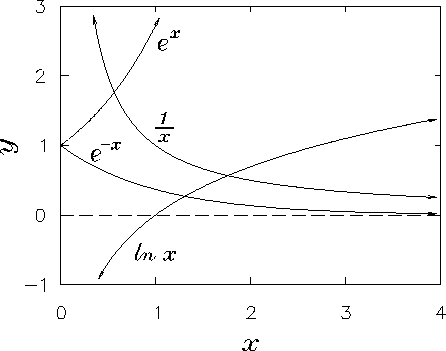
, you can be sure that
where y0 is the ``initial value'' of y [when x=0]. Note that k can be either positive or negative.