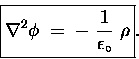- A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE
The EQUATION OF CONTINUITY (see above) describes
the conservation of ``actual physical stuff''
entering or leaving an infinitesimal region of space dV.
For example, ![]() may be the current density
(charge flow per unit time per unit area normal to the direction of flow)
in which case
may be the current density
(charge flow per unit time per unit area normal to the direction of flow)
in which case ![]() is the charge density
(charge per unit volume); in that example the conserved ``stuff''
is electric charge itself. Many other examples exist,
such as FLUID DYNAMICS (in which mass is the conserved stuff)
or HEAT FLOW (in which energy is the conserved quantity).
In ELECTROMAGNETISM, however, we deal not only with the
conservation of charge but also with
the continuity of abstract vector fields
like
is the charge density
(charge per unit volume); in that example the conserved ``stuff''
is electric charge itself. Many other examples exist,
such as FLUID DYNAMICS (in which mass is the conserved stuff)
or HEAT FLOW (in which energy is the conserved quantity).
In ELECTROMAGNETISM, however, we deal not only with the
conservation of charge but also with
the continuity of abstract vector fields
like ![]() and
and ![]() .
In order to visualize
.
In order to visualize ![]() ,
we have developed the notion of
``electric field lines'' that cannot be broken except where they
originate (from positive charges) and terminate (on negative charges).
[This description only holds for static electric fields;
when things move or otherwise change with time,
things get a lot more complicated . . . and interesting!]
Thus a positive charge is a ``source of electric field lines''
and a negative charge is a ``sink'' - the charges themselves
stay put, but the lines of
,
we have developed the notion of
``electric field lines'' that cannot be broken except where they
originate (from positive charges) and terminate (on negative charges).
[This description only holds for static electric fields;
when things move or otherwise change with time,
things get a lot more complicated . . . and interesting!]
Thus a positive charge is a ``source of electric field lines''
and a negative charge is a ``sink'' - the charges themselves
stay put, but the lines of ![]() diverge out of or into them.
You can probably see where this is heading.
diverge out of or into them.
You can probably see where this is heading.
GAUSS' LAW states that the net flux of electric field ``lines''
out of a closed surface ![]() is proportional to the
net electric charge enclosed within that surface.
The constant of proportionality depends on which system of units
one is using; in SI units it is
is proportional to the
net electric charge enclosed within that surface.
The constant of proportionality depends on which system of units
one is using; in SI units it is
![]() .
In mathematical shorthand, this reads
.
In mathematical shorthand, this reads
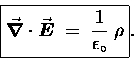
Poisson and Laplace
Even in its differential form, GAUSS' LAW is a little
tricky to solve analytically, since it is a vector
differential equation. Generally we have an easier time
solving scalar differential equations,
even though they may involve higher order partial derivatives.
Fortunately, we can convert the former into the latter:
recall that the vector electric field can always
be obtained from the scalar electrostatic potential using