BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: The Wave Equation
Up: Maxwell's Equations
Previous: Ampère's Law
In 1865, James Clerk Maxwell assembled all the known ``Laws''
of in their most compact, elegant (differential) form,
shown here in SI units:
GAUSS' LAW FOR ELECTROSTATICS:
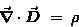 |
(22.9) |
GAUSS' LAW FOR MAGNETOSTATICS:
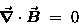 |
(22.10) |
FARADAY'S LAW:
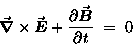 |
(22.11) |
AMPÈRE'S LAW:
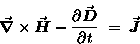 |
(22.12) |
These four basic equations are known collectively
as MAXWELL'S EQUATIONS; they are considered by most Physicists
to be a beautifully concise summary of phenomenology.
Well, actually, a complete description of
also requires two additional laws:
EQUATION OF CONTINUITY:
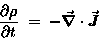 |
(22.13) |
LORENTZ FORCE:
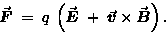 |
(22.14) |


Next: The Wave Equation
Up: Maxwell's Equations
Previous: Ampère's Law
Jess H. Brewer
1999-04-07
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE