- . . . error).5.1
- More on this later . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . thing;5.2
- ``Uncertainty'' is somewhere in between.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
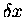 ?5.3
?5.3
- Notational convention:
we use
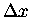 to denote ``a change in x, not necessarily tiny''
whereas
to denote ``a change in x, not necessarily tiny''
whereas 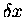 usually means ``a little bitty change in x,
but definitely finite!'' and dx means ``a change in x that is
so teensy that it can be neglected relative to anything else but
another really teensy thing.'' That last one (dx) is called
a ``differential'' - Mathematicians don't like it much but
Physicists use it all the time.
usually means ``a little bitty change in x,
but definitely finite!'' and dx means ``a change in x that is
so teensy that it can be neglected relative to anything else but
another really teensy thing.'' That last one (dx) is called
a ``differential'' - Mathematicians don't like it much but
Physicists use it all the time.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
by:5.4
- The symbol
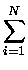 represents an operator called ``summation'' -
it means that {the stuff to the right of the
represents an operator called ``summation'' -
it means that {the stuff to the right of the 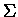 },
which will always have a subscript i in one or more places,
is to be thought of as the ``
},
which will always have a subscript i in one or more places,
is to be thought of as the ``
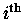 term'' and
all such terms with i values running from 1 to N
are to be added together to form the desired result.
So, for instance,
term'' and
all such terms with i values running from 1 to N
are to be added together to form the desired result.
So, for instance,
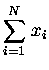 means
means
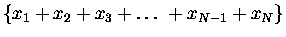 ,
or (to be more specific) if N=3, just
,
or (to be more specific) if N=3, just
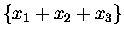 .
This may seem a little arcane, but it is actually a very handy
compact notation for the rather common summation operation.
.
This may seem a little arcane, but it is actually a very handy
compact notation for the rather common summation operation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE