BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: Statics
Up: Torque and Angular Momentum
Previous: A Moment of Inertia, Please!
It is, however, worth remembering that all the now-familiar [?]
paradigms and equations of Mechanics come in ``rotational analogues:''
LINEAR
VERSION |
ANGULAR
VERSION |
NAME |
| x |
 |
angle |
 |
 |
 |
 |
 |
 |
| m |
IO |
 |
 |
 |
 |
| F |
 |
torque |
 |
 |
SECOND LAW |
 |
 |
 |
 |
 |
 |
| F = - k x |
 |
 |
 |
 |
 |


Next: Statics
Up: Torque and Angular Momentum
Previous: A Moment of Inertia, Please!
Jess H. Brewer
1998-10-08
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE 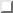 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE 




