BELIEVE   ME   NOT!    - -     A   SKEPTICs   GUIDE  

. . . paradigm.^13.1

Many people are so taken with this paradigm that they apply it to all experience. The I Ching, for instance, is said to be based on the ancient equivalent of ``tuning in'' to the ``vibrations'' of Life and the World so that one's awareness resonates with the universe. By New Age reckoning, cultivating such resonances is supposed to be the fast track to enlightenment. Actually, Physics relies very heavily on the same paradigm and in fact supports the notion that many apparently random phenomena are actually superpositions of regular cycles; however, it offers little encouragement for expecting ``answers'' to emerge effortlessly from such a tuning of one's mind's resonances. Too bad. But I'm getting ahead of myself here.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . word.^13.2

Examples of cyclic but not necessarily periodic phenomena are the mass extinctions of species on Earth that seem to have occurred roughly every 24 million years, the ``seven-year cycle'' of sunspot activity, the return of salmon to the river of their origin and recurring droughts in Africa. In some cases the basic reason for the cycle is understood and it is obvious why it only repeats approximately; in other cases we have no idea of the root cause; and in still others there is not even a consensus that the phenomenon is truly cyclic - as opposed to just a random fluctuation that just happens to mimic cyclic behaviour over a short time. Obviously the resolution of these uncertainties demands ``more data,'' i.e. watching to see if the cycle continues; with the mass extinction ``cycle,'' this requires considerable patience. When ``periodicity debates'' rage on in the absence of additional data, it is usually a sign that the combatants have some other axe to grind.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . axle.^13.3

Note the frequency with which we periodically recycle our paradigms!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . motion.^13.4

Although we have become conditioned to expect such mathematical formulations of relationships to be more removed from our intuitive understanding than easily visualized concrete examples like the projection of circular motion, this is a case where the mathematics allows us to draw a sweeping conclusion about the detailed behaviour of any system that exhibits certain simple properties. Furthermore, these conditions are actually satisfied by an incredible variety of real systems, from the atoms that make up any solid object to the interpersonal ``distance'' in an intimate relationship. Just wait!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . holds:^13.5

You may find this unremarkable, but I have never gotten over my astonishment that functions so ostensibly unrelated as the exponential and the sinusoidal functions could be so intimately connected! And for once the mathematical oddity has profound practical applications.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . them.^13.6

I am reminded of a passage in one of Kurt Vonnegut's books, perhaps Sirens of Titan, in which the story of creation is told something like this: God creates the world; then he creates Man, who sits up, looks around and says, ``What's the meaning of all this?'' God answers, ``What, there has to be a meaning?'' Man: ``Of course.'' God: ``Well then, I leave it to you to think of one.''

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . i.e.^13.7

The ``$\gg$'' symbol means `` . . . is much greater than . . . '' - there is an analogous ``$\ll$'' symbol that means `` . . . is much less than . . . . ''

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . .  or^13.8

There is a general rule about exponents that says, ``A number raised to the sum of two powers is equal to the product of the same number raised to each power separately,'' or

$$a^{b+c} = a^b \cdot a^c .$$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . frequency^13.9

The word ``complex'' has, like ``real'' and ``imaginary,'' been ripped off by Mathematicians and given a very explicit meaning that is not entirely compatible with its ordinary dictionary definition. While a complex number in Mathematics may indeed be complex - i.e. complicated and difficult to understand - it is defined only by virtue of its having both a real part and an imaginary part, such as 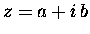  $z = a + i \, b$,  where  a  and  b  are both real. I hope that makes everything crystal clear . . . .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . counterintuitive.^13.10

It is, after all, one of the main purposes of this book to dismantle your intuition and rebuild it with the faulty parts left out and some shiny new paradigms added.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . oscillation.^13.11

Of course, this assumes 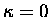  $\kappa = 0$.  If damping occurs at the same time, we must put at least as much energy in with our driving force as friction takes out through the damping in order to build up the amplitude. Almost every system has some limiting amplitude beyond which the restoring force is no longer linear and/or some sort of losses set in.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

. . . resonance^13.12

(something like you get from a blade of grass held between the thumbs to create a loud noise when you blow past it)

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.