


Next: Propagation of Errors
Up: No Title
Previous: Normal Distribution
Sometimes it is not practical to make the large number of measurements needed
to calculate accurate estimates of the mean and standard deviation; instead,
just one measurement is available to use as the estimate of the true value. In
this case you must use your judgement to estimate the uncertainty in this
measurement. Several factors enter into this, some of which could be the
following.
- The uncertainty may come from how accurately you can read a measuring
device. For example, the accuracy with which you could read a ruler would
depend on how closely spaced its tick marks are, and on how steadily it could
be held while the
measurement was being made.
- There may be fluctuations in the conditions under which an
experiment was done which could affect the outcome of the experiment but which
were beyond the control of the observer. These might include variations in the
room temperature or the line voltage.
- Your model of the physical situation may be somewhat unrealistic, so that
no matter how precisely measurements are made, calculations using
these measurements will not give an accurate result because the formulae aren't
a totally accurate model of reality. An example of this would be a calculation
of the range of a projectile using a formula that neglects air
resistance: the result might be fairly accurate for a bullet but not for
a wad of paper, no matter how precisely you measure its initial velocity.
You must take the various factors into consideration and then exercise
your best judgement in estimating the range within which you are confident that
the measurement lies. The hope is that for random errors the estimate of
the uncertainty that you make this way would be comparable to the value of
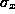 you would obtain if you made the measurement several times.
you would obtain if you made the measurement several times.



Next: Propagation of Errors
Up: No Title
Previous: Normal Distribution
![]() you would obtain if you made the measurement several times.
you would obtain if you made the measurement several times.