THE UNIVERSITY OF BRITISH COLUMBIA
Physics 122
Assignment #
4:
GAUSS' LAW
Fri. 25 Jan. 2002 - finish by Fri. 1 Feb.
- 1.
- GAUSS' LAW FOR A SHEET OF CHARGE:
Imagine an infinite plane sheet of electric charge
with
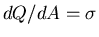 units of charge per unit surface area.
Using your own words and drawings,1
units of charge per unit surface area.
Using your own words and drawings,1
- (a)
- Using only (i) the SUPERPOSITION PRINCIPLE
for the total electric field due to an assembly of
electric charges, plus (ii) simple
SYMMETRY arguments, deduce the direction
of the electric field due to the plane of charge.
- (b)
- Using the preceding result plus the general
ideas of GAUSS' LAW and simple geometry,
deduce the dependence of the
magnitude E of the electric field upon x,
the perpendicular distance away from the plane.
- (c)
- Show that your result agrees with the x-dependence of
the electric field on axis due to a uniform disc of charge
when
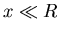 ,
the radius of the disc.
,
the radius of the disc.
- 2.
- FIELD WITHIN A UNIFORM CHARGE DISTRIBUTION:
The textbook shows how to use GAUSS' LAW to derive the
radial (r) dependence of the electric field E(r>R)
outside charge distributions of
spherical, cylindrical or planar symmetry,
where R is the distance the charge distribution extends
from the centre of symmetry - the radius of a
charged sphere or cylinder, or half the thickness
of an infinite slab of charge, respectively.
Use similar arguments to show that, for each of these cases
(a sphere, cylinder or a slab of uniform charge density),
the electric field E(r<R) inside the charge distribution
is given in terms of the field E(R) at the boundary
of the charge distribution by
- 3.
- ATOMS AS SPHERES OF CHARGE:
In Rutherford's work on
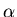 particle scattering from atomic nuclei,
he regarded the atom as having a pointlike positive charge of +Ze
at its centre, surrounded by a spherical volume of radius R filled
with a uniform charge density that makes up a total charge -Ze.
In this simple model, calculate the electric field strength E
and the electric potential
particle scattering from atomic nuclei,
he regarded the atom as having a pointlike positive charge of +Ze
at its centre, surrounded by a spherical volume of radius R filled
with a uniform charge density that makes up a total charge -Ze.
In this simple model, calculate the electric field strength E
and the electric potential 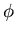 as functions of radius r and various constants.
Plot your results for
as functions of radius r and various constants.
Plot your results for
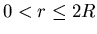 .
(Choose
.
(Choose
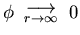 .)
.)
Jess H. Brewer
2002-01-22
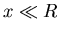 ,
the radius of the disc.
,
the radius of the disc.