ANSWER:
Start with no charge, then bring successive bits dQ in to add
uniformly to the charge Q of the shell. A given bit of charge
acquires an electrostatic potential energy
dE = kE QdQ/r0
in the process. Thus the total energy E required to assemble the
shell is
![]() . If we set
this equal to m c2 we get
. If we set
this equal to m c2 we get
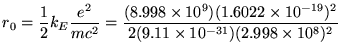 or
or
![]() . The conventional value
(actually the Compton wavelength of the electron) is twice as big,
2.818 fm, where ``fm'' stands for ``femtometers'' or ``fermis''
(named after Enrico Fermi); both are the same as 10-15 m.
. The conventional value
(actually the Compton wavelength of the electron) is twice as big,
2.818 fm, where ``fm'' stands for ``femtometers'' or ``fermis''
(named after Enrico Fermi); both are the same as 10-15 m.
ANSWER:
The original capacitance was
![]() . The capacitor with
the insert as shown is equivalent to two identical capacitors in
series, each of which has a gap of d/4 between its plates,
so that
C1 = C2 = 4 C. The equivalent capacitance of two
capacitors in series is given by
. The capacitor with
the insert as shown is equivalent to two identical capacitors in
series, each of which has a gap of d/4 between its plates,
so that
C1 = C2 = 4 C. The equivalent capacitance of two
capacitors in series is given by
![]() . Thus
. Thus
![]() .
.
- (a)
- the capacitance of the resulting cube-shaped capacitor;
ANSWER:
Each layer consists of 2 sheets of Cu and 1 sheet of SrTiO3
and so is 250 µm or
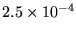 m
thick. The number of layers is therefore
m
thick. The number of layers is therefore
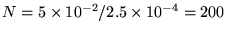 and the
total area is
and the
total area is
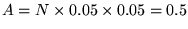 m2.
The capacitance is
m2.
The capacitance is
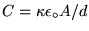 where d = 150 µm.
The dielectric constant of SrTiO3 is (from Table 27-2)
where d = 150 µm.
The dielectric constant of SrTiO3 is (from Table 27-2)
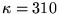 , so
, so
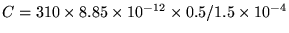 or
or
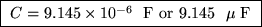 .
.
- (b)
- the maximum charge it will hold without breaking down;
ANSWER:
Table 27-2 lists the dielectric strength of SrTiO3 as 8 kV/mm,
which is the same as
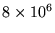 V/m. Our dielectric sheet
has a thickness of
V/m. Our dielectric sheet
has a thickness of
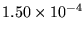 m, so the breakdown
voltage is 1200 V. At that potential, Q = CV gives
m, so the breakdown
voltage is 1200 V. At that potential, Q = CV gives
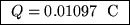 .1
.1
- (c)
- the total energy we can store in this small cube.
ANSWER:
The total energy stored in a capacitor is given by
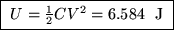 .
.
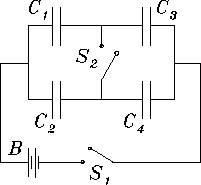
The battery B supplies 6 V. The capacitances are C1 = 2.0 µF, C2 = 1.0 µF, C3 = 4.0 µF and C4 = 3.0 µF.
- (a)
- Find the charge on each capacitor
when switch S1 is closed but switch S2 is still open.
ANSWER:
Let Qi denote the charge on the
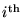 capacitor Ci.
From charge conservation we have Q1 = Q3 and Q2 = Q4.
Both pairs of capacitors in series (1 and 3; 2 and 4) must make up
the full voltage:
VB = Q1/C1 + Q3/C3 = Q2/C2 + Q4/C4.
Therefore
VB = Q1[1/C1 + 1/C3] = Q2[1/C2 + 1/C4]
yielding
Q1 = Q3 = 6/(106/2.0 + 106/4.0) and
Q2 = Q4 = 6/(106/1.0 + 106/3.0) or
capacitor Ci.
From charge conservation we have Q1 = Q3 and Q2 = Q4.
Both pairs of capacitors in series (1 and 3; 2 and 4) must make up
the full voltage:
VB = Q1/C1 + Q3/C3 = Q2/C2 + Q4/C4.
Therefore
VB = Q1[1/C1 + 1/C3] = Q2[1/C2 + 1/C4]
yielding
Q1 = Q3 = 6/(106/2.0 + 106/4.0) and
Q2 = Q4 = 6/(106/1.0 + 106/3.0) or
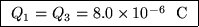 and
and
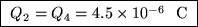 .
.
- (b)
- What is the charge on each capacitor if S2 is also closed?
ANSWER:
Now C1 and C2 are effectively just one big capacitor
C12 = C1 + C2 = 3.0 µF and similarly for
C34 = C3 + C4 = 7.0 µF. Charge conservation
now requires
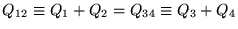 and the two effective capacitors in series must make up the
full voltage:
VB = Q12/C12 + Q34/C34.
Thus
VB = Q12[1/C12 + 1/C34] giving
and the two effective capacitors in series must make up the
full voltage:
VB = Q12/C12 + Q34/C34.
Thus
VB = Q12[1/C12 + 1/C34] giving
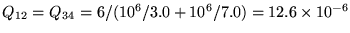 C.
Meanwhile the voltage across C1 must be the same as that across C2:
C.
Meanwhile the voltage across C1 must be the same as that across C2:
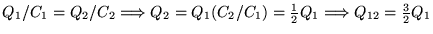 or
or
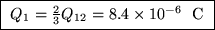 and
and
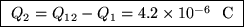 .
Similarly,
.
Similarly,
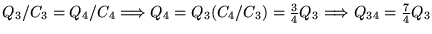 or
or
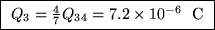 and
and
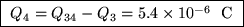 .
.
- (a)
- Estimate the number of Coulombs [C] of positive charge
in the cloud, assuming that the ground has the same surface density
of negative charge.
ANSWER:
The electric field between two flat plates with surface charge densities
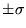 is given by
is given by
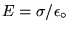 . Thus
. Thus
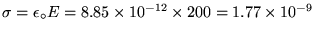 C/m2.
Over an area of
C/m2.
Over an area of
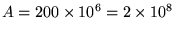 m2,
this gives a total charge of
m2,
this gives a total charge of
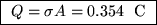 .
.
- (b)
- Estimate the number of joules [J] of energy
contained in the air between the cloud and the ground.
ANSWER:
The energy density stored in an electric field is given by
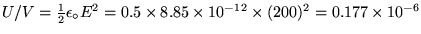 J/m3. The volume between the cloud
and the ground is
J/m3. The volume between the cloud
and the ground is
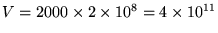 m3, so
m3, so
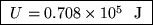 .
.