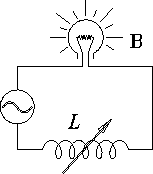
- (a)
- What maximum inductance L is required if the power in the
light bulb is to be varied by a factor of five?
ANSWER:
Since we are looking for a given power ratio,
the answer will be independent of the rms driving voltage (see below).
The frequency is
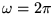 (60 Hz) = 377 s-1.
The light bulb draws
(60 Hz) = 377 s-1.
The light bulb draws
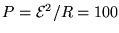 W
when the voltage drop across it is
W
when the voltage drop across it is
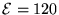 V,
so
V,
so
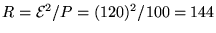
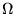 .
Now, for an LR circuit the impedance is just
.
Now, for an LR circuit the impedance is just
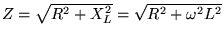 (i.e. we just omit the capacitive reactance term)1
so that
(i.e. we just omit the capacitive reactance term)1
so that
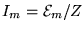 and the average power
dissipated in the resistance (light bulb) is
and the average power
dissipated in the resistance (light bulb) is
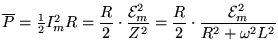 .
When
.
When 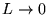 we get a maximum value of
we get a maximum value of
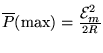 and when
and when
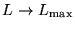 we get a minimum value of
we get a minimum value of
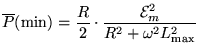 .
We want the ratio of these to be five:
.
We want the ratio of these to be five:
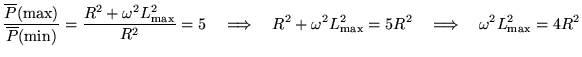 or
or
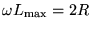 giving
giving
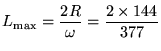 or
or
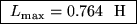 .
.
- (b)
- Could one use a variable resistor in place of the
variable inductor? If so, what maximum resistance R
would be required? Why isn't this done?
(Variable resistors [rheostats] are generally
cheaper than variable inductors.)
ANSWER:
The circuit would be cheaper to build using a rheostat in place
of the variable inductance and it would work fine:
the two resistances in series would just add up to one net resistance
 so that
so that
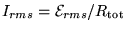 and
and
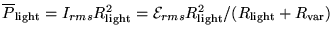 ,
which can be varied from a minimum of
,
which can be varied from a minimum of
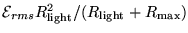 to a maximum of
to a maximum of
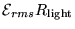 ,
the ratio of which
,
the ratio of which
![$[R_{\rm light}/(R_{\rm light} + R_{\rm max})]$](img23.gif) can easily be made equal to 5.
The problem with this simpler design is that when the light is
dimmed (
can easily be made equal to 5.
The problem with this simpler design is that when the light is
dimmed (
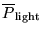 minimized),
considerable power
minimized),
considerable power
![$[I_{rms} R_{\rm var}^2]$](img25.gif) is being uselessly dissipated in the rheostat!
A pure inductance, by contrast, does not draw any power;
it merely shifts the phase of the voltage and current.
is being uselessly dissipated in the rheostat!
A pure inductance, by contrast, does not draw any power;
it merely shifts the phase of the voltage and current.
(a)
(b)
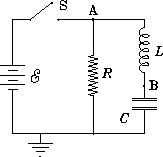
ANSWER: This problem has a tricky part, namely the behaviour when the switch is first closed. In this situation
When the switch is opened again, we do get different behaviour depending on the ratio of R to L. Specifically, if we define
where
- (a)
- Write expressions for all three components of the magnetic field
associated with the wave.
ANSWER: The wave propagates in the direction given by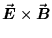 (see textbook's section on the POYNTING VECTOR) and so, since
(see textbook's section on the POYNTING VECTOR) and so, since
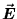 points in the
points in the 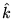 direction and the wave propagates in the
direction and the wave propagates in the
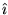 direction, we must have
direction, we must have
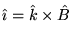 where
where 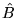 is the unit vector in the
is the unit vector in the 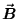 direction. The only unit vector
satisfying this criterion is
direction. The only unit vector
satisfying this criterion is
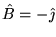 and so
and so 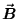 is in the negative y direction
when
is in the negative y direction
when 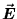 is in the positive z direction.
Both must oscillate sinusoidally with the same wavelength
and frequency, so they share the same propagation speed c,
the same wavenumber k and the same angular frequency
is in the positive z direction.
Both must oscillate sinusoidally with the same wavelength
and frequency, so they share the same propagation speed c,
the same wavenumber k and the same angular frequency
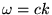 .
This allows us to write down the answer:
.
This allows us to write down the answer:
![\fbox{ $B_x = B_z = 0$\space ~ and ~
$ B_y = - B_0 \sin[k(x - ct)] $\space }](img53.gif) .
.
Having established this, we need only find the relationship between the amplitudes of the E and B fields. Their magnitudes must satisfy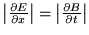 ,
giving
,
giving
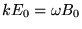 or
or
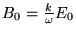 or
or
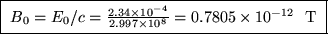 .
(This also follows from E=cB [always valid].)
.
(This also follows from E=cB [always valid].)
- (b)
- Find the wavelength of the wave.
ANSWER:
All you need for this part is the universal relationship
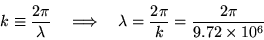
or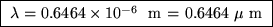 .
.