BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: Canonical Variables
Up: ``Solving'' the Motion
Previous: ``Solving'' the Motion
If the equation of motion is the ``question,''
what constitutes an ``answer''?
Surely the most convenient thing to know about
any given problem is the explicit time dependence of the position,
x(t), because if we want the velocity
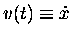 ,
all we have to do is take the first time derivative - which may not
be entirely trivial but is usually much easier than integrating!
And if we want the acceleration
,
all we have to do is take the first time derivative - which may not
be entirely trivial but is usually much easier than integrating!
And if we want the acceleration
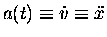 ,
all we have to do is take the time derivative again.
Once you have found the acceleration, of course,
you also know the net force on the object,
by NEWTON'S SECOND LAW.
A problem of this sort is therefore considered ``solved''
when we have discovered the explicit function x(t)
that ``satisfies'' the equation of motion.
,
all we have to do is take the time derivative again.
Once you have found the acceleration, of course,
you also know the net force on the object,
by NEWTON'S SECOND LAW.
A problem of this sort is therefore considered ``solved''
when we have discovered the explicit function x(t)
that ``satisfies'' the equation of motion.
For example, suppose we know that
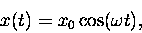 |
(12.5) |
where 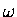 is some constant with units of radians/unit time,
so that
is some constant with units of radians/unit time,
so that 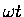 is an angle.
The time derivative of this is the velocity
is an angle.
The time derivative of this is the velocity
[look it up if needed] and the time derivative of that
is the acceleration
Note that the right-hand side of the last equation is just
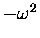 times our original formula for x(t), so we can
also write
times our original formula for x(t), so we can
also write
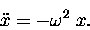 |
(12.6) |
Multiplying through both sides by
the mass m of the object in motion gives
which ought to look familiar
to you: it is just HOOKE'S LAW with a force constant
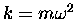 .
Rearranging this a little gives
.
Rearranging this a little gives
which may also look familiar . . . .
More on this later. Note, however, that we can very easily
deduce what is going on in this situation, including the
type of force being applied, just from knowing x(t).
That's why we think of it as ``the solution.''


Next: Canonical Variables
Up: ``Solving'' the Motion
Previous: ``Solving'' the Motion
Jess H. Brewer
1998-10-08
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE ![]() ,
all we have to do is take the first time derivative - which may not
be entirely trivial but is usually much easier than integrating!
And if we want the acceleration
,
all we have to do is take the first time derivative - which may not
be entirely trivial but is usually much easier than integrating!
And if we want the acceleration
![]() ,
all we have to do is take the time derivative again.
Once you have found the acceleration, of course,
you also know the net force on the object,
by NEWTON'S SECOND LAW.
A problem of this sort is therefore considered ``solved''
when we have discovered the explicit function x(t)
that ``satisfies'' the equation of motion.
,
all we have to do is take the time derivative again.
Once you have found the acceleration, of course,
you also know the net force on the object,
by NEWTON'S SECOND LAW.
A problem of this sort is therefore considered ``solved''
when we have discovered the explicit function x(t)
that ``satisfies'' the equation of motion.