BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: Timing is Everything!
Up: Equations of Motion
Previous: Equations of Motion
Getting back to the subject of Mechanics . . .
One of the reasons the paradigms in the previous chapter emerged
was that physicists were always trying to ``solve'' certain types
of ``problems'' using Newton's SECOND LAW,12.4
This equation can be written
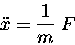 |
(12.1) |
to emphasize that it described a relationship between
the acceleration 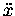 ,
the inertial coefficient m [usually constant]
and the force F.
It is conventional to call an equation in this form
the ``equation of motion'' governing the problem at hand.
When F is constant [as for ``local'' gravity]
the ``solution'' to the equation of motion
is the well-known set of equations governing
constant acceleration, covered in the chapter on FALLING BODIES.
Things are not always that simple, though.
,
the inertial coefficient m [usually constant]
and the force F.
It is conventional to call an equation in this form
the ``equation of motion'' governing the problem at hand.
When F is constant [as for ``local'' gravity]
the ``solution'' to the equation of motion
is the well-known set of equations governing
constant acceleration, covered in the chapter on FALLING BODIES.
Things are not always that simple, though.
Sometimes the problem is posed in such a way that
the force F is explicitly a function of time,
F(t). This is not hard to work with, at least in principle,
since the equation of motion (1) is then in the form
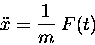 |
(12.2) |
which can be straightforwardly integrated
[assuming one knows a function whose time derivative is F(t)]
using the formal operation
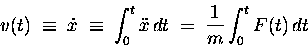 |
(12.3) |
-- which, when multiplied on both sides by m,
leads to the paradigm of Impulse and Momentum.
In other cases the problem may be posed in such a way that
the force F is explicitly a function of position,
F(x). Then the equation of motion has the form
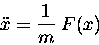 |
(12.4) |
which can be converted without too much trouble
[using the identity
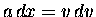 ]
into the paradigm of Work and Energy.
]
into the paradigm of Work and Energy.


Next: Timing is Everything!
Up: Equations of Motion
Previous: Equations of Motion
Jess H. Brewer
1998-10-08
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE