BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: Bohr's Energy Levels
Up: Fudging The Bohr Atom
Previous: Fudging The Bohr Atom
We can play more games with Bohr's hydrogen atom if we like,
using just Eq. (8) to relate rn and pn.
Suppose we ask, ``What is keeping the electron in its orbit?''
The answer is, of course, ``The Coulomb force of attraction
between the positive nucleus and the negative electron!''
This centripetal force has the value (in SI units)
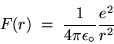 |
(24.10) |
where
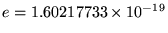 C
is the magnitude of the charge on either an electron
(-e) or a proton (+e) and the ugly mess out front is the legacy
of SI units - a constant stuck in to make it come out right.
The corresponding electrostatic potential energy is
C
is the magnitude of the charge on either an electron
(-e) or a proton (+e) and the ugly mess out front is the legacy
of SI units - a constant stuck in to make it come out right.
The corresponding electrostatic potential energy is
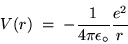 |
(24.11) |
(relative to 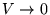 at
at
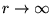 ).
We'll need that momentarily.
).
We'll need that momentarily.
A simple application of NEWTON'S SECOND LAW gives
where m is the mass of the electron.
Cancelling one r and rearranging gives
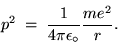 |
(24.12) |
Substituting Eq. (8) into Eq. (12) gives
or (after some shuffling)
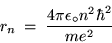 |
(24.13) |
for the radius of the
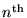 Bohr orbit of the H atom.
The lowest orbit (n = 1) has a special name and symbol:
the BOHR RADIUS,
Bohr orbit of the H atom.
The lowest orbit (n = 1) has a special name and symbol:
the BOHR RADIUS,
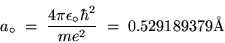 |
(24.14) |
where 1 Å = 10-10 m.


Next: Bohr's Energy Levels
Up: Fudging The Bohr Atom
Previous: Fudging The Bohr Atom
Jess H. Brewer
2000-01-17
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE