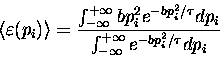- . . . Physics15.1
- I have ``borrowed''
the notation, general approach, basic derivations and
most of the quotations shown here from the excellent
textbook of the same name by Kittel & Kroemer,
who therefore deserve all the credit (and none of the blame)
for the abbreviated version displayed before you.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . way,15.2
- In
the present case, we have a choice of whether
to treat the pennies as ``indistinguishable'' or not.
No two pennies are really indistinguishable,
of course; even without our painted-on numbers,
each one has unique scratches on its surface
and was crystallized from the molten state in a unique
microscopic pattern. We could tell one from another;
we just don't care, for circumstantial reasons.
In QUANTUM MECHANICS, however, you will encounter the concept of
elementary particles [e.g. electrons] which
are so uncomplicated that they truly are
indistinguishable [i.e. perfectly identical];
moreover, STATISTICAL MECHANICS provides a means
of actually testing to see whether they are
really absolutely indistinguishable or just very similar!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . tails.15.3
- It might be
that we get to keep all the pennies that come up heads,
but for every penny that comes up tails
we have to chip in another penny of our own.
In that case our profit would be
n - (N-n) = 2n - N cents.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . filled].15.4
- If you
were the parking lot owner and were charging $1
per space [cheap!], your profit would be $n. I keep
coming back to monetary examples - I guess cash
is the social analogue of energy in this context.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . particles,15.5
- The term ``particle''
is [in this usage] meant to be as vague as possible, just like
``system:'' the particles are ``really simple things
that are all very much alike''
and the system is ``a bunch of particles taken together.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . plotted15.6
- Actually
what is plotted in Fig. 15.1 is
the probability function
vs.
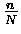 ,
as explained in the caption.
Otherwise it would be difficult to put more than one plot
on the same graph, as the peak value of
,
as explained in the caption.
Otherwise it would be difficult to put more than one plot
on the same graph, as the peak value of
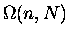 gets very large very fast as N increases!
gets very large very fast as N increases!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
variance15.7
- Recall
your Physics Lab training on MEASUREMENT!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . huge.15.8
- A good estimate of the
size of N! for large N is given by
Stirling's approximation:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . paradigm15.9
- Count on it!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ``particles''15.10
- Remember,
a ``particle'' is meant to be an abstract concept in this context!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . other.15.11
- If I
flip my coin once and you flip your coin twice,
there are 21 = 2 ways my flip can go [h, t]
and 22 = 4 ways your 2 flips can go [HH, HT, TH, TT];
the total number of ways the combination
of your flips and mine can go
[hHH, hHT, hTH, hTT, tHH, tHT, tTH, tTT]
is
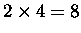 .
And so on.
.
And so on.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . states15.12
- Nothing precludes
finding the system in states with other values of U1,
of course. In fact we must do so sometimes!
Just less often.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . follows:15.13
- Perhaps the converse is actually true:
human ``wants'' are actually manifestations of random
processes whose variety is greater in the direction
of perceived desire. I find this speculation disturbing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
assumptions.15.14
- Or, at least,
none that are readily apparent . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . configuration15.15
- Note
the distinction between the words configuration
and state. The latter implies we specify everything
about the system - all the positions and velocities of
all its particles, etc. - whereas the former refers only
to some gross overall macroscopic specification
like the total energy or how it is split up between two
subsystems. A state is completely specified
while a configuration is only partly specified.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . entropy.15.16
- This is the same
as maximizing the probability, but from now on I want to use
the terminology ``maximizing the entropy.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . mathematics.15.17
- We have
already done this once, but it bears repeating!
To avoid complete redundancy, this time we will
reverse the order of hot and cold.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . was!15.18
- Well, to be fair, people had
a pretty good working knowledge of the properties
of temperature; they just didn't have a definition
of temperature in terms of nuts-and-bolts mechanics, like
Eq. (10).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . degrees15.19
- These silly units were invented by
an instrument maker called Fahrenheit [1686-1736]
who was selling thermometers to meteorologists.
He picked body temperature [a handy reference,
constant to the precision of his measurements]
for one ``fiducial'' point and for the other he picked
the freezing point of saturated salt water,
presumably from the North Sea. Why not pure water?
Well, he didn't like negative temperatures
[neither do we, but he didn't go far enough!]
so he picked a temperature that was,
for a meteorologist, as cold as was worth measuring.
[Below that, presumably, it was just ``damn cold!'']
Then he (sensibly) divided up the interval between these
two fiducials into 96=64+32 equal ``degrees'' [can you see
why this is a pragmatic choice for the number of divisions?]
and voilá! he had the Fahrenheit temperature
scale, on which pure water freezes at 32
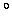 F
and boils at 212
F
and boils at 212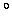 F.
A good system to forget, if you can.
F.
A good system to forget, if you can.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ``Kelvin''15.20
- Named after
Thomson, Lord Kelvin [1852], a pioneer of thermodynamics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . field.15.21
- The
rate of change of this energy with the angle
between the field and the compass needle is in fact the
torque which tries to align the compass in the Earth's
magnetic field, an effect of considerable practical value.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . laboratory.15.22
- [by reversing
the direction of the magnetic field
before the spins have a chance to react]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . system15.23
- A
``small system''
can even be a ``particle,'' since both terms
are intentionally vague and abstract enough
to mean anything we want!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ``atoms,''15.24
- I will cover
the history of ``Atomism'' in a bit more detail later on!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . suggest,15.25
- If
you want the details, here they are:
Suppose that pi is the CANONICAL MOMENTUM
characterizing the
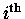 degree of freedom of a system and
that
degree of freedom of a system and
that
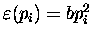 is the energy associated with
a given value of pi.
Assume further that pi can have a continuous
distribution of values from
is the energy associated with
a given value of pi.
Assume further that pi can have a continuous
distribution of values from 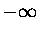 to
to 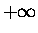 .
Then the probability of pi having a given value is
proportional to
.
Then the probability of pi having a given value is
proportional to
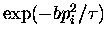 and therefore the
average energy associated with that degree of freedom is
given by
and therefore the
average energy associated with that degree of freedom is
given by
These definite integrals have ``well known'' solutions:
where in this case
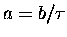 and x = pi,
giving
and x = pi,
giving
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . argument15.26
- We
can, of course, make the explanation more elaborate,
thus satisfying both the demands of rigourous logic
and the Puritan conviction that nothing of real value
can be obtained without hard work. I will leave this
as an exercise for other instructors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
pressure15.27
- Unfortunately, we use the same
notation (p) for both momentum and pressure.
Worse yet, the notation for number density
(number of atoms per unit volume) is n.
Sorry, I didn't set up the conventions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . sum.15.28
- We may say that
the average kinetic energy ``stored in the
x degree of freedom'' of an atom
is
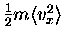 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . write15.29
- This is equivalent to
saying that the average energy stored in the
x degree of freedom of one atom
[or, for that matter, in any other degree of freedom]
is
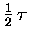 -- which is just what we originally claimed
in the EQUIPARTITION THEOREM. We could have just jumped to this
result, but I thought it might be illuminating to show an explicit argument
for the equality of the mean energies
stored in several different degrees of freedom.
-- which is just what we originally claimed
in the EQUIPARTITION THEOREM. We could have just jumped to this
result, but I thought it might be illuminating to show an explicit argument
for the equality of the mean energies
stored in several different degrees of freedom.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE