- . . . surface.14.1
- Technically
speaking, I couldn't have picked a worse example,
since water waves do not behave like our idealized
example - a cork in the water does not move straight
up and down as a wave passes, but rather in a vertical circle.
Nevertheless I will use the example for illustration because it is
the most familiar sort of easily visualized wave for most people
and you have to watch closely to notice the difference anyway!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
SHM).14.2
- Note that
 would have worked just as well, since the real part is the same
as for
would have worked just as well, since the real part is the same
as for
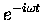 .
The choice of sign
does matter, however, when we write down the combined
time and space dependence in Eq. (4), which see.
.
The choice of sign
does matter, however, when we write down the combined
time and space dependence in Eq. (4), which see.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . vector;14.3
- The name ``wave vector''
is both apt and inadequate - apt because the term vector
explicitly reminds us that its direction defines the direction of
propagation of the wave; inadequate because the essential inverse
relationship between k and the wavelength
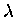 [see Eq. (1)] is not suggested by the name. Too bad.
It is at least a little more descriptive than the name given to
the magnitude k of
[see Eq. (1)] is not suggested by the name. Too bad.
It is at least a little more descriptive than the name given to
the magnitude k of 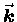 ,
namely the ``wavenumber.''
,
namely the ``wavenumber.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . that14.4
- In general
 .
If
.
If
 then kx = k and
ky = kz = 0,
giving
then kx = k and
ky = kz = 0,
giving
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . wave14.5
- Don't
try this with an electromagnetic wave! The argument shown here is
explicitly nonrelativistic, although a more mathematical
proof reaches the same conclusion without such restrictions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . . 14.6
- The Figure
could also describe standing sound waves in an organ pipe
closed at both ends, or the electric field strength in a resonant cavity,
or the probability amplitude of an electron confined to a one-dimensional
``box'' of length L.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . half-wavelengths:14.7
- Note that
the
 mode has (n-1) nodes
in addition to the two at the ends.
mode has (n-1) nodes
in addition to the two at the ends.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . have14.8
- I
have avoided complex exponentials here to avoid
confusion when I get around to calculating the
transverse speed of the string element, vy.
The acceleration is the same as for the
complex version.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . lives,14.9
- Indeed,
we are made of waves,
as QUANTUM MECHANICS has taught us!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . shakes.14.10
- Note also that any of s, ds, P or dP
can be either positive or negative; we merely illustrate the math
using an example in which they are all positive.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . correct.14.11
- I should probably
show you a few wrong guesses first, just to avoid giving
the false impression that we always guess right the first time
in Physics; but it would use up a lot of space for little
purpose; and besides, ``knowing the answer'' is always the
most powerful problem-solving technique!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . outgoing14.12
- One can
also have ``incoming'' spherical waves, for which
Eq. (38) becomes
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Cartesian14.13
- The LAPLACIAN
operator can also be represented in other coordinate systems
such as spherical (
 )
or cylindrical (
)
or cylindrical (
 )
coordinates, but I won't get carried away here.
)
coordinates, but I won't get carried away here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . as14.14
- The LAPLACIAN operator
can also be thought of as the inner (scalar or ``dot'') product
of the GRADIENT operator
 with itself:
with itself:
 , where
, where
in Cartesian coordinates. This VECTOR CALCULUS stuff is
really elegant - you should check it out sometime -
but it is usually regarded to be beyond the scope of
an introductory presentation like this.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . frequencies.14.15
- If the wavelength
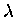 increases (so that the wavenumber
increases (so that the wavenumber
 decreases), then the frequency
decreases), then the frequency 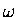 must
decrease to match, since the ratio
must
decrease to match, since the ratio  must always be equal to the same propagation velocity c.
must always be equal to the same propagation velocity c.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . on.14.16
- One can detect a history of proponents
of different bands claiming ever higher (and therefore presumably
``better'') frequency ranges . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . particles.14.17
- He
was actually correct, but it is equally true that light
consists of waves. If you are hoping that these apparently
contradictory statements will be reconciled with common sense
by the Chapter on QUANTUM MECHANICS, you are in for a
disappointment. Common sense will have to be beaten into
submission by the utterly implausible facts.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . slowly.14.18
- Boy,
is this ever Aristotelian!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . LAW:14.19
- SNELL'S LAW is normally expressed
in terms of the INDEX OF REFRACTION n in each medium:
where (we now know) the INDEX OF REFRACTION is the ratio
of the speed of light in vacuum to the speed of light in the medium:
The reason for inventing such a semicircular definition
was that when Willebrord Snell discovered this empirical
relationship in 1621 he had no idea what n was, only
that every medium had its own special value of n.
(This is typical of anything that gets the name ``index.'')
I see no pedagogical reason to even define the dumb thing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . continuous14.20
- A
``crest'' doesn't turn into a ``trough'' just because
the propagation velocity changes!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . origin.14.21
- This
is sort of like the mathematical assertion
that all lines look straight if we look at them
through a powerful enough microscope.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . light.14.22
- ``Corpuscles''
are hypothetical particles of light that follow trajectories
Newton called ``rays,'' thus starting a long tradition of naming
every new form or radiation a ``ray.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE 