BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: The Wave Equation
Up: Wave Phenomena
Previous: Traveling Waves
Neither of the images in Fig. 14.1 captures the most important
qualitative feature of the wave: namely, that it propagates
-- i.e. moves steadily along in the direction of
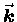 .
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
.
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
The wave has a distance 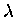 (one wavelength)
between ``crests.'' Every period T, one full
wavelength passes a fixed position. Therefore a given crest
travels a distance
(one wavelength)
between ``crests.'' Every period T, one full
wavelength passes a fixed position. Therefore a given crest
travels a distance 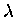 in a time T so the velocity
of propagation of the wave is just
in a time T so the velocity
of propagation of the wave is just
 |
(14.6) |
where I have used c as the symbol for the propagation velocity
even though this is a completely general relationship
between the frequency 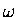 ,
the wave vector magnitude k
and the propagation velocity c of any sort of wave,
not just electromagnetic waves (for which c has
its most familiar meaning, namely the speed of light).
,
the wave vector magnitude k
and the propagation velocity c of any sort of wave,
not just electromagnetic waves (for which c has
its most familiar meaning, namely the speed of light).
This result can be obtained more easily by noting that
A is a function only of the phase
 of the oscillation,
of the oscillation,
 |
(14.7) |
and that the criterion for ``seeing the same waveform''
is  constant or
constant or
 .
If we take the differential of Eq. (7)
and set it equal to zero, we get
.
If we take the differential of Eq. (7)
and set it equal to zero, we get
But dx/dt = c, the propagation velocity of the waveform.
Thus we reproduce Eq. (6).
This treatment also shows why we chose
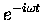 for the
time dependence so that Eq. (7)
would describe the phase: if we used
for the
time dependence so that Eq. (7)
would describe the phase: if we used
 then the
phase would be
then the
phase would be
 which gives
dx/dt = -c, - i.e. a waveform
propagating in the negative x direction
(to the left as drawn).
which gives
dx/dt = -c, - i.e. a waveform
propagating in the negative x direction
(to the left as drawn).
If we use the relationship (6) to write
 , so that Eq. (4)
becomes
, so that Eq. (4)
becomes
we can extend the above argument to waveforms that are not
of the ideal sinusoidal shape shown in Fig. 14.1;
in fact it is more vivid if one imagines some special
shape like (for instance) a pulse
propagating down a string at velocity c.
As long as A(x,t) is a function only of
x' = x - ct,
no matter what its shape, it will be static in time
when viewed by an observer traveling along with the wave14.5
at velocity c. This doesn't require any elaborate derivation;
x' is just the position measured in such an observer's reference frame!


Next: The Wave Equation
Up: Wave Phenomena
Previous: Traveling Waves
Jess H. Brewer
1998-11-06
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE ![]() .
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
.
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
![]() (one wavelength)
between ``crests.'' Every period T, one full
wavelength passes a fixed position. Therefore a given crest
travels a distance
(one wavelength)
between ``crests.'' Every period T, one full
wavelength passes a fixed position. Therefore a given crest
travels a distance ![]() in a time T so the velocity
of propagation of the wave is just
in a time T so the velocity
of propagation of the wave is just
![]() of the oscillation,
of the oscillation,
![]() , so that Eq. (4)
becomes
, so that Eq. (4)
becomes