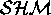 ) using
a simple pendulum. Examples of
) using
a simple pendulum. Examples of 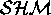 are found in many systems: oscillations of any system
around a stable equilibrium point
can usually be well-approximated in terms of
are found in many systems: oscillations of any system
around a stable equilibrium point
can usually be well-approximated in terms of 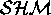 .
.
In this part of the experiment you will study
simple harmonic motion (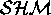 ) using
a simple pendulum. Examples of
) using
a simple pendulum. Examples of 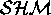 are found in many systems: oscillations of any system
around a stable equilibrium point
can usually be well-approximated in terms of
are found in many systems: oscillations of any system
around a stable equilibrium point
can usually be well-approximated in terms of 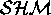 .
.
Consider a simple pendulum consisting of a mass m
suspended by a string of length l as shown below.
Assume that the string is at an angle
![]() with respect to the vertical.
with respect to the vertical.
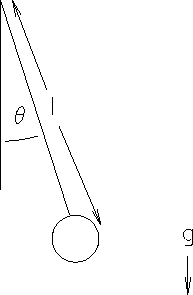
Figure 2.7: Simple Pendulum
The net torque acting on the mass, taking the point where the string is suspended as our origin, is given by
![]()
The moment of inertia I of the system is
![]()
The instantaneous angular acceleration is therefore given by

If the angle
![]() is small (say less than 15
is small (say less than 15
![]() radians), then
radians), then
![]() ,
where
,
where
![]() is measured in radians.
We can then rearrange the above differential equation for
is measured in radians.
We can then rearrange the above differential equation for
![]() to obtain:
to obtain:
![]()
This is the equation for a simple harmonic oscillator
(![]() ).
).
We can solve this equation by guessing the form of the solution,
then substituting back into the equation.
Guided by our knowledge of a mass on a spring
(another system which obeys the 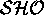 equation),
we anticipate a solution where
the angle
equation),
we anticipate a solution where
the angle ![]() is a sinusoidal function of time.
The most general such solution is given by
is a sinusoidal function of time.
The most general such solution is given by
![]()
We can differentiate this equation twice to obtain
![]()
then substitute the result into the equation. Doing this, we find that
![]()
The values of
![]() and
and ![]() depend on the initial conditions, they correspond
to the amplitude of the oscillation
(the maximum angle reached)
and the phase of the oscillations
(essentially depending on when we choose for the time t=0
relative to the motion of the pendulum).
depend on the initial conditions, they correspond
to the amplitude of the oscillation
(the maximum angle reached)
and the phase of the oscillations
(essentially depending on when we choose for the time t=0
relative to the motion of the pendulum).