A small constant force can be applied to
the rider by inclining the track slightly. The
component of gravity which acts on the rider
parallel to the air-track is equal to ![]() ,
as indicated in Fig. 2.5.
,
as indicated in Fig. 2.5.
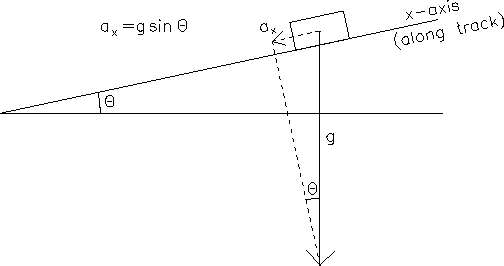
Figure 2.5:
Geometry for rider on air-track with a small angle.
Use a few of the shims provided to elevate the right side of the air-track.
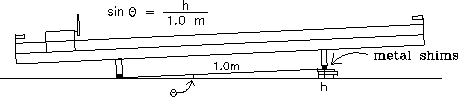
Figure 2.6
From this one series of measurements of the rider's position, there are many ways to analyze the data and calculate the acceleration of the rider. All of these ways are mathematically related, but for each one you are isolating and analyzing different pieces of the data, so the correspondence between different calculations will not be exact. There are four methods which you should consider:
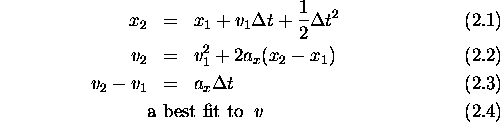
Analyzing the data you just collected,
calculate the value of
![]() ,
and in turn g, using
different data points from the graph
for each of the equations above. Is your calculation
of g close to the accepted value?
,
and in turn g, using
different data points from the graph
for each of the equations above. Is your calculation
of g close to the accepted value?
Perform the same analysis on two more trials. For the first, use a different inclination of the air-track. For the second, start with the rider at the bottom of the track (using either inclination) and after you begin taking data, give it a gentle push up the track.
Can you observe any significant deviation in the results obtained from these different trials? Which of the four methods seems most accurate? Using all of your results, what is your average calculated value of g?