Next: 6.3 Lenses
Up: Geometrical Optics
Previous: 6.1 Reflection
The velocity of light in free space is very close to
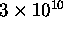 cm/s;
moreover, the velocity is the same for all wavelengths.
The situation is different in most material substances.
With few exceptions, the velocity of light in material substances
is less than the velocity in free space.
Not only is the velocity less, it varies with the
wavelength of the light passing through the medium.
cm/s;
moreover, the velocity is the same for all wavelengths.
The situation is different in most material substances.
With few exceptions, the velocity of light in material substances
is less than the velocity in free space.
Not only is the velocity less, it varies with the
wavelength of the light passing through the medium.
If light travels through two media with different velocities,
the wave nature of the light causes its direction to be
altered as it passes from one medium into the other.
This phenomenon is referred to as refraction.
We can define the index of refraction (n) of a material
to be the ratio of the velocity of light in free space (c)
to its velocity in the given material (v).
Since the velocity (v) varies with wavelength,
we must specify the corresponding wavelength
when referring to an index of refraction.
The purpose of this portion of the experiment
is to determine the relation between
the direction of the incident ray, the direction of the refracted ray,
and the index of refraction. The index of glass (for example) varies
by less than 2% throughout the visible spectrum. Therefore, using
the incandescent light source (rather than a single frequency laser source)
doesn't introduce much error.
- Take a square piece of millimeter graph paper about 5 cm on a side.
Place the paper between the glass plate and the special component carrier on
the angular translator. The magnetic surface will hold the glass plate
and paper in place.
- Adjust the position of the special component carrier
until the back surface of the glass plate
coincides with the perpendicularly scored line on the table.
- With the glass plate sitting perpendicular to the bench,
adjust the position of the aperture mask
so that one vertical edge of the image on the paper
lines up with the scored line on the table
which is parallel to the bench.
If the glass does not alter the lights's path,
the vertical edge which was centered should remain centered
although the translator's table is rotated.
- Rotate the table and record what happens to
the previously centered edge. Is the incident ray
refracted toward or away from the normal to the glass?
Before arriving for the experiment,
work out how to calculate the index of refraction given
the angle of rotation and the edge displacement of the image
using the quantities shown in Fig. D.
Note: Using this method, a small error is introduced since we are
not certain that the light very near to the image's edge was
exactly perpendicular to the glass plate in the beginning.
(Why?) Hence the measured value of
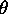 (as shown in Fig. D is not accurate.
The method in the following section gives more accurate results.
(as shown in Fig. D is not accurate.
The method in the following section gives more accurate results.
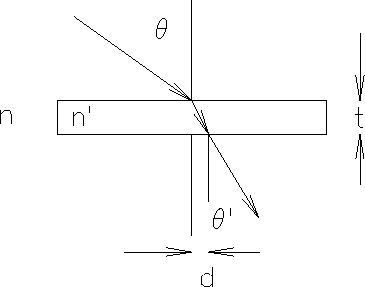
Figure D: Calculating the index of refraction.
- Remove the paper from between the glass plate and component carrier.
With the glass place perpendicular to the bench,
put the viewing screen directly behind the plate
and adjust the aperture mask to center the image on the screen.
Rotate the table to a convenient angle.
Light is refracted toward the normal when passing from air to glass.
Is the same true when light propagates from
glass to air? By observing the position of the image
on the viewing screen, you can see that the refraction
must be away from the normal at a
glass-air interface (see Figure E).
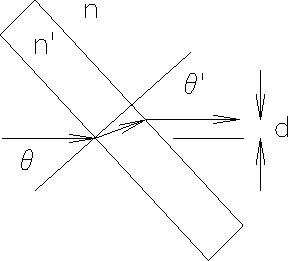
Figure E: Index of refraction: improved method.
- Remove the special component carrier
from the angular translator table
and replace it with the
 prism.
prism.
- With the scored lines running perpendicular and parallel to the bench,
position the prism so that one of the small faces is centered on
the table and coincides with the perpendicularly scored line.
- Check the position of the aperture mask
so that the center of the light beam travels
directly over the center of the table and parallel to the bench.
- Move the arm until the refracted beam is imaged on the viewing screen.
Now rotate the table and watch the movement of the image (move the arm if
necessary). Although the prism is continually rotated in the same direction,
note that the image moves in one direction and then begins moving in the other
direction. The point where the image reverses direction coincides with the
angle of minimum deviation. That is, at that particular angle of incidence
the light beam is deviated least from its original path.
- From the angle of minimum deviation,
calculate the index of refraction of the prism material.
Before coming to the lab,
work out how to find the index of refraction
from the measured minimum deviation angle.
Note: The edges of the image are colored. Why? This phenomenon
is called dispersion.
- Rotate the table until the refracted beam
is parallel to the large surface (slanted surface) of the prism.
In this position, no light propagates through
the slanted surface; all of the light is internally reflected.
- Knowing the angle of incidence
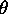 we can calculate the angle of
incidence
we can calculate the angle of
incidence
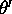 of the light in the prism as it
reaches the slanted surface. The angle
of the light in the prism as it
reaches the slanted surface. The angle
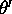 is called the critical angle.
is called the critical angle.
- The
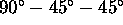 prism is designed so that any light
normal to the slanted surface is totally internally reflected.
Position the prism to observe this phenomenon.
prism is designed so that any light
normal to the slanted surface is totally internally reflected.
Position the prism to observe this phenomenon.
Next: 6.3 Lenses
Up: Geometrical Optics
Previous: 6.1 Reflection
![]() cm/s;
moreover, the velocity is the same for all wavelengths.
The situation is different in most material substances.
With few exceptions, the velocity of light in material substances
is less than the velocity in free space.
Not only is the velocity less, it varies with the
wavelength of the light passing through the medium.
cm/s;
moreover, the velocity is the same for all wavelengths.
The situation is different in most material substances.
With few exceptions, the velocity of light in material substances
is less than the velocity in free space.
Not only is the velocity less, it varies with the
wavelength of the light passing through the medium.
![]() (as shown in Fig. D is not accurate.
The method in the following section gives more accurate results.
(as shown in Fig. D is not accurate.
The method in the following section gives more accurate results.