RC Transients

When a voltage is applied to a series R-C circuit, the charge q across C rises asymptotically to and the current i decays from its initial value towards zero. The rise of q and the fall of i both involve the same exponential function of time.

The value is called the ``time constant'' of the circuit.

Connect the square wave generator, which alternatively places a fixed voltage and a short circuit across a series RC circuit for equal time intervals, as shown in Fig. 9.4. The rise and decay of i can then be observed by using the oscilloscope to measure the voltage across R as a function of time. [The oscilloscope measures V(t); therefore i(t)=V(t)/R.] Be sure to connect your circuit so that the square wave generator and the oscillator share a common ground.

   

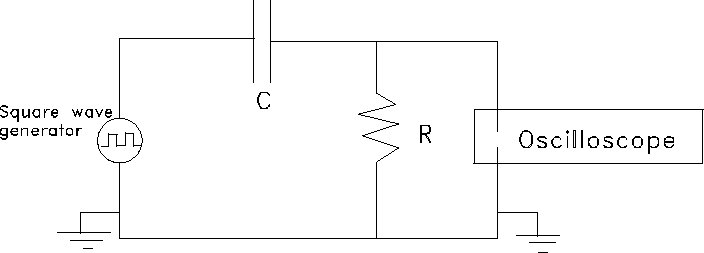
Figure 9.4: - Square wave generator to measure RC time constant.

Adjust the period of the square wave generator to allow several time constants between consecutive ``switching'' and adjust the sweep time of the oscilloscope to observe the rise and decay of the current.

Measure by determining the time it takes the current to fall to 1/e of its initial value.

The variation of the charge on the capacitor may be observed by using the oscilloscope to measure the voltage across C:

Reconnect your circuit, again making sure that the square wave generator and the oscilloscope share a common ground.

  
Figure 9.5: - Measuring .

1. Sketch graphs of q(t) and i(t), using a common time (horizontal) axis.
2. Compare your measured with the expected values from the given values of R and C.
3. What is the shortest value of you could conveniently measure with this technique? Explain briefly.

The value of will depend on the internal resistance of the square wave generator as well as the external resistor used: . The internal resistance can be measured in the following way:

1. Connect the oscilloscope directly across the generator and measure the voltage .
2. Connect the oscilloscope across the generator when it is connected in parallel with a resistor r and measure the voltage .
3. Adjust r until . Then, . Explain why this is true.